Working with Google's Cartographer SLAM Package

At my current position, at Canvas Construction, I have worked with a number of SLAM and localization packages. In the past few years, my worked has focused on using Cartographer for mapping indoor environments. Since Canvas is still a stealth company, I will not dive into why we need to map, but suffice it to say, we need a strong understanding of our environment.

Our setup includes two Velodyne VLP-16 LIDAR's, a mid-range IMU and wheel encoder odometry mounted to a mobile robot. This sensor data is collected as the robot moves around its environment, and is fed through the Cartographer algorithm (online). Cartographer is not meant to be an online algorithm, but can be tuned for low latency and for our purposes that has worked fine. After a sufficient amount of mapping is performed, the sensor data is fed through the "Assets Writer", which aligns poses from the pose graph with the sensor data, hence building both a 2D map and 3D point cloud of the space. These maps have been found to be accurate to about 2-5 cm of error.

The Cartographer algorithm works in two parts. The first is known as Local SLAM and consists of:

• A pose estimate created by scan matching the incoming laser range data
• The insertion of that laser range data into a "submap"

The idea is to create many submaps over time that can be related to each other with constraints.  The part of the algorithm that relates these submaps is called Global SLAM. It consists of:

• Creating constraints between parts of individual submaps (inter-submap). These are simply differences in poses after a significant movement.
• Creating constraints between different submaps (intra-submap). These constraints are the difference between poses that exist on multiple submaps or are close-enough. They help to connect the different submaps together.
• Performs Global Optimization by way of "sparse pose adjustment". This algorithm uses the computed constraints and tries to move each submap around so that it can meet the created constraints with minimal error.
• Finally, it extrapolates all of the poses onto the newly created map with minimal error.

This is an image of the algorithm from the Cartographer website.

After mapping, we output a point cloud that looks like this, showing the area that we mapped: 

As I have become more familiar with the Cartographer package, I have learned about some tricks and pitfalls that have come up. 

• The Cartographer algorithm has shown to be very sensitive to IMU location. Even the slightest discrepancy between the true and modeled locations can cause major warping of the submaps, especially when using Cartographer 3D, which we do.
• Tuning of Cartographer is challenging because there are many knobs to turn. Especially because the values of the tuned parameters are often dimensionless scalar values that multiply against relative errors.
• The latency can be reduced with the corresponding effect of reducing the accuracy of the maps.
• If the effect of scan matching is tuned well, the odometry can have a very small impact on the resulting map.
• The orientation of the LIDAR has a strong effect on the results of the map. In our use case, we are using a horizontal and vertical LIDAR in order to see the full space around the robot and a vertical strip that gives more of the ceiling and floor. This turned out to work better than angling the LIDAR more non-overlapping visibility.

Thanks for reading!

Update To AHRS with Mag!

Since my previous post on AHRS types, I have made some additional changes to the three systems.  Specifically, I have added the magnetometer data as an update to the yaw in each system.  My technique for adding the mag in each system was derived from this paper by Sebastian Madgwick. 

The idea is that the Earth's magnetic field can be described as having a components in a single horizontal axis and a single vertical axis.  By rotating these components inversely, by our quaternion, we can directly compare our results to the measured magnetic field vector.  This was especially helpful because it simplified the equation for R in the EKF and UKF, because I could directly use square of the rms-noise of the magnetometer sensors as the diagonals of the matrix. 

The toughest part of this problem was deriving each of the equations for Madgwick, the EKF and the UKF.  I would post it my work, but it is extremely tedious.  However, the results are very good and you can see that it clearly improved the yaw from the previous post in all three cases.

This was an extremely exciting result for me to see, because I worked very hard on the solutions.  The one area that I need to work on is when to provide updates to the EKF and UKF.  Currently, I use an accelerometer threshold, just to make sure there is no movement.  However, this causes the system to be very sensitive to slight movements.  Preferably, I would like to make a more robust system for performing updates.  That's all for now!

Testing Some AHRS Algorithms

https://github.com/team401/Vision-Tutorials/wiki/Yaw-and-Pitch

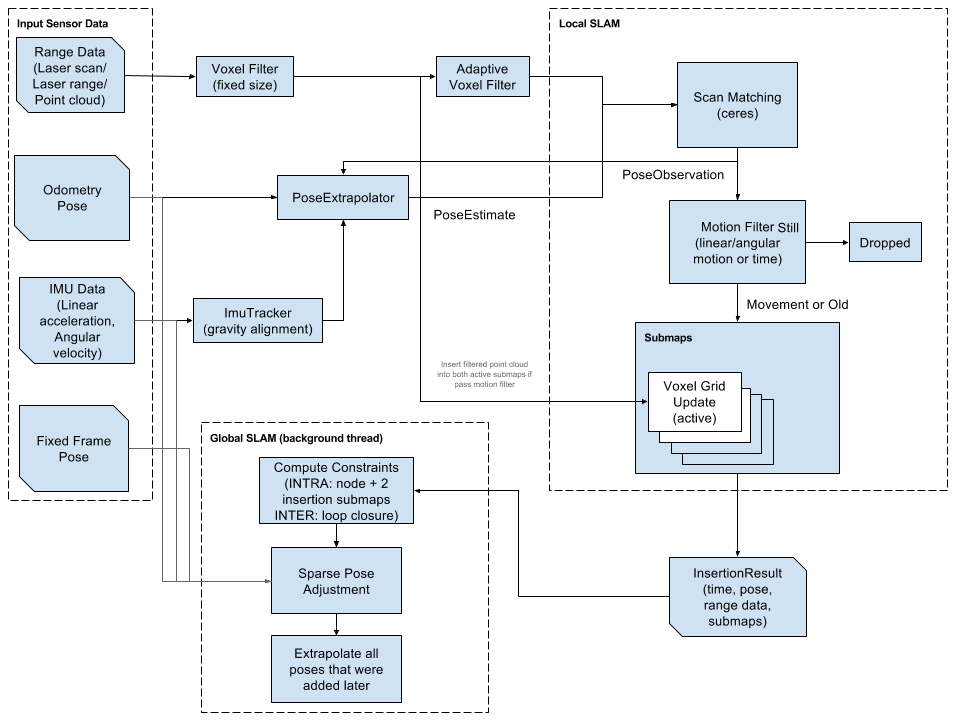
In recent weeks, I have spent some time brushing up on as many types of Attitude and Heading Reference Systems (AHRS) as I can.  I wanted to code them, and compare them in a meaningful way and eventually implement them on an Arduino.  My initial goal has been to work with three types: The Madgwick Filter, an Extended Kalman Filter and an Unscented Kalman Filter.  As of right now, I have each of them working and am able to play back a few different types of csv datasets.  All of my code is on my github.

I should note that I collected data from my phone, which is a Google Pixel, that holds a BMI160 IMU sensor with a 3 axis accelerometer, 3 axis gyroscope, 3 axis magnetometer, a barometer and a temperature sensor.  I am sampling the data using an app called HyperIMU (available on the Google Play Store).  As of right now, I have only integrated the gyroscope and the accelerometer and am working on the magnetometer updates.

All of my implementations are very simple models, that do not yet introduce the gyroscope bias as parameter in the filter.  This will be added later, because it complicates the model.  My states are the quaternion values: w, x, y, z and all operations are done in quaternion space in order to avoid the singularity when the pitch is at 90 degrees.

The Madgwick Filter

The Madgwick Filter is based on this paper by Sebastian Madgwick.  Remarkably, it is a very new algorithm, but has been widely used across many systems.  The idea of this filter is to incorporate updates to the classic gyroscope integration via an optimization assumption.  The initial update is to correct for drift in the pitch and roll directions by taking advantage of the direction of gravity from the accelerometers.  Essentially, the algorithm forms an objective function between the gravitational vector rotated into the frame of the sensor and the acceleration vector in the frame of the sensor.  The idea is that at all times, the acceleration is an approximation of the gravity, even though there may be some acceleration due to movement and noise.  The optimization is solved with a gradient descent solution and is therefore, always attempting to correct any drift originating from the gyroscope in the gravity related directions.  

Here is an image of the results of the Madgwick filter when applied to my phone spinning along the three axes.  This is particular run is using the recommended beta gain value from the paper, however, I have found that setting it to between 0.04 and 0.2, allows it to converge faster and more accurately.   

As you can see in the image, the prediction of roll, pitch and yaw works well. In the roll and pitch directions, you can see that the filter is slowly converging back to 0 degrees.  If I increase the beta value, I can speed up that convergence, but it comes at the cost of factoring in any acceleration that is not due to gravity.  To see the divergence, I decided to compare residual between the estimate and the measurement.  What is interesting to see is what happens when we have actual movement of the phone and how it causes divergence in the filter values. 

The Extended Kalman Filter

The EKF is the standard equation for most estimation problems and it fits well for the AHRS, as well.  Essentially, the EKF is a typical Kalman filter that linearizes the prediction and update equations in order to estimate the uncertainty of each of the states.  The uncertainty is used to weight measurement updates in order to shrink the overall error of the system.  When the sensor is moving with extra acceleration, the gravity updates are far more damaging than they are in the Madgwick filter.  In order to mitigate this problem, I decided to only apply updates when the change in acceleration along all three axes is less than a threshold. This way, we know that the phone is stationary during this period.  In the future, I will work on a more robust way to find allowable update times.

Here is the results of the EKF.  The Euler plot shows fast convergence back to 0 degrees in the pitch and roll after rotations.  We can see a bit more noise in the solution than Madgwick Filter, but faster convergance.  This is probably because the linearized function does not approximate the uncertainty distribution as well.

I have only plotted the residuals when I have done updates.  As you can see, the residual is zero mean and has a nice error distribution after the updates.  This means that the filter is doing its job.

The Unscented Kalman Filter

The UKF was a curious addition to this batch of algorithms.  Typically, a UKF is used if there is an unclear distribution function.  It works by creating a distribution from a few "Sigma Points", which are projections of the system states with a fraction of the noise added back in.  This creates a pseudo space that approximates the distribution of the uncertainty of each state.  

This image was very helpful in my understanding of the UKF.  Basically, a proportion of the standard deviation of the uncertainty is added to each state and then either projected forward in time by the state transition matrix or rotated to the measurement frame.

https://github.com/rlabbe/Kalman-and-Bayesian-Filters-in-Python/blob/master/10-Unscented-Kalman-Filter.ipynb

Here are the results of the UKF.  Again, we are seeing good results in terms of convergence back to zero after large movements in pitch and roll.  We also see that we have somewhat Gaussian Error in the residual.  

Here are the histograms of the Roll and Pitch error.  Both are very Gaussian and has almost exactly the same amount of mean and error as the EKF.  

Now that I have this done, I have a few other things that I want to do to improve my results.  These things include:

• Yaw correction via Magnetometer
• Gyroscope bias correction, also with the Magnetometer and possibly the Temperature Sensor
• Process and Measurement noise improvement via adaptive EKF
• Implementation in C for realtime estimation on Arduino

Update On RNN's for Predicting Crypto Prices

This is a Recurrent Neural Network diagram from here

Sporadically, I have been working on this little project to both learn more about recurrent neural networks and build something useful to predict future cryptocurrency prices.  As I talked about before, I have been looking into ways of predicting the price on a rolling basis.  As of right now, I am predicting the next day's price from a history of 6 days before.  Let's take a look at what I did.

Recurrent Neural Networks are a good choice for this type of timeseries because they can incorporate new values and keep track of history in order to make new predictions.  I am using Keras to create the network and here is how I built it:

lookback=6
model = Sequential()
batch_size = 1
model.add(LSTM(4, input_shape=(lookback, 1)))
model.add(Dense(1))
model.compile(loss='mse', optimizer='rmsprop', metrics=['mae'])

As you can see, I used 4 Long-Short Term Memory blocks and a lookback of 6 days.  I used "rmsprop" as my optimizer because it is essentially a more advanced gradient descent method which is usually fine for regression tasks.  The Loss Metric chosen was Mean Square Error, which is the classic loss function for regression problems.  I am also keeping track of Mean Absolute Error, just to confirm the results.

The data in this example consists of BTC/USD daily closes from January 2016 to February 2018.  This is the plot of that data.

Before training, I scale the data between 0 and 0.9 to account for higher prices in the future, with a Min-Max Scaler from Sci-kit Learn.  In the future, I may try dividing by 1 million instead, to better account for future prices (I don't see it hitting 1 million any time soon, but it could in the future).   Then I split the data into training and testing datasets with a 67% training split.  During the train, I also check a 20% validation set, just to watch how each iteration of the model performs.  I have plotted these values during the train.  This allows me to see at what point the model begins to over-train. We can see this by looking at the point at which the validation loss (MSE) significantly diverges from the training loss.  This is an image of that plot, with the validation loss filtered to discard noise:

In this example, I have trained to 1000 iterations.  It is kind of tough to see the divergence, but it happens around 125 iterations.  I am curious if I were to leave it training for 10,000 iterations, whether there might be a more clear divergence point.  Anyway, if we train to about 125 iterations, we get a result that looks like the one below.  The green line is the prediction of trained data and the red line is the prediction of the untrained portion of the data.  Although the result is clearly worse, I am pretty happy with how well it did.  

The results are as follows: 

- On Trained data the RMSE is 44.67

- On Test data the RMSE is 1342.08

The question is, how can I improve this result?  My initial thoughts are to experiment with different look-back values, and possibly more LSTM blocks.  However, I suspect that the most practical way to improve the result is to also add in open's, high's and low's as features as well.  This may vastly improve the model because it will be able to see momentum and other patterns at each timestep.  This where I will focus next.

Check out my code here: https://github.com/Sanderi44/crypto-analysis

Some Computer Vision For Kicks

Over the past few weeks, I have been working on a few different projects to broaden my skills and learn about some new technologies.  One area that I have been jumping into is computer vision.  Recently, I have been working my way through the book "OpenCV with Python Blueprints".  Some of the projects I have done so far include building a Cartoonizer and some Feature Matching.  Let me show you!

This is me just after finishing the Cartoonizer.  As you can see, the program cartoonizes live video and shows the result in real-time.  The process involves:
- Applying a bilateral filter in order to smooth flat areas while keeping edges sharp
- Converting the original to grayscale
- Applying a median blur to reduce image noise
- Using an adaptive threshold to detect edges
- Combining the color image with the edge mask

The result is really great!

Another project I just completed is the Feature Matching project.  The idea here is to find robust features of an image, match them in another image and find the transform that converts between the two images.

Here is an examples of what that looks like in practice.  On the left, is the still image that I took from my computer and on the right is a live image of the scene.  The red lines show where the feature in the first frame is located in the second frame. This seemed to work pretty well for very similar scenes, but had some trouble when I changed the scene significantly.  However, it is not unexpected that it would fail on different scenes, because the features are not very similar at all.

Here is how I did it:
- First I used SURF (Speeded-Up Robust Features) to find some distinctive keypoints.
- Then, I used FLANN (Fast Library for Approximate Nearest Neighbors) to check whether the other frame has similar keypoints and then match them.
- Then, using outlier rejection, I was able to pare down the number of features to only the good ones.
-  Finally, using a perspective transform, I was able to warp the second image so that it matched the first (not shown here).

I am currently in the middle of the 3D scene reconstruction project.  This something I have been meaning to do for a long time and I am currently really enjoying working on it.

Cryptocurrency Analysis

It's been a while since I last posted, because I was working hard over at Navisens.  After about 3 years, I am now back on the market looking for a new position.  In the meantime, I have started working on another project that has fascinated me for a while.

For about a year now, I have been looking into and trading cryptocurrencies.  I find the whole market exciting to follow and very lucrative (if you do it right).  This is where my new project comes in.   I am building a tool for querying historical cryptocurrency price data in order to analyze and use it for making future price predictions.  My current progress is located on my Github.

To get started, I have built a simple api that uses the phenomenal ccxt api to query from tons of exchanges to build up data. Then, once I have a significant amount of data, I will test some machine learning algorithms on that data.

Here are some questions that I am starting to think about:

- How is one cryptocurrency related to another?  Can I use the data from one crypto to train a classifier/regressor for predicting a different crypto?

- What type of Machine Learning algorithms will work best on this time-series data? Neural Networks? Recurrent Neural Networks?  Decision Trees? Bayesian Estimators?

- What features should I use as inputs to the ML algorithms?  Do I need scaling? (probably)  How many features will be sufficient?

- What should I predict? A new price (regressor)? Whether it will go up or down (classifier)?

As I start to look at these problems more carefully, I will continue to write about the conclusions that I come to.  If you have questions or thoughts, I would love to hear them! Feel free to comment on this post or send me an email!

A Kalman Filter for a Robot Car

This past week, I have spent quite a bit of time working on a simulator for a two-wheel differential drive robot.  The idea was to use simulated encoder and range finder data and an Extended Kalman filter to determine the location of a robot.  My implementation is written in Python and hosted here.

The system is modeled as having two inputs - The left and right wheel speeds.  The robot is externally given control inputs, but they are unknown to the Kalman filter.  The only inputs to the Kalman filter system are the encoder values and the range finder values and a set of known landmarks (this is to simulate mapping or some other landmark detection).  The encoder inputs are Vl and Vr.  From these values, we can surmise the average velocity V, and the rotational velocity w of the robot.

V = (Vl + Vr)/2

w = (Vr - Vl)/L, where L = length between wheels 

We can then use the image below to determine the simple version of the equations of motion of the robot.

An image of a differential drive robot.

From this system, we can surmise that the equations of motion, in discrete form, are:

x(k+1) = x(k) + V(k)*Cos(theta(k))*dt
y(k+1) = y(k) + V(k)*Sin(theta(k))*dt
theta(k+1) = theta(k)  + w(k)*dt

This means that we can assign the system states to be X, Y and Theta.  Because the system model above is ideal, we also need to add in a Gaussian noise value for each state. Now the system looks like this:

x(k+1) = x(k) + (V(k) + Nv) *Cos(theta(k))*dt
y(k+1) = y(k) + (V(k) + Nv) *Sin(theta(k))*dt
theta(k+1) = theta(k)  + (w(k) + Nw)*dt

The Kalman filter has two steps. The prediction step, and the update step.  The prediction step uses the system model, previous state values and control inputs (in this case, encoder values) to create a prediction (a priori) of the new states of the system.  It also creates an estimate covariance matrix, that is essentially a mathematical way to determine how much you trust the sensor values and the prediction.  The matrices needed for the calculation of the prediction step are the A, G, Q and P matrices.  A is the Jacobian, with respect to the system states, for the model shown above.  G is the Jacobian with respect to the noise values.  Q is a matrix built up by the covariances of the process noise.   The prediction step equations are:

X^(k+1) = f (X(k), U(k)) , where f (X(k), U(k)) is the original system model
P^(k+1) = A*P(k)*transpose(A) + G*Q*transpose(G)

The update step (a posteriori) is a bit more complicated.  The idea is to use a separate sensor (or multiple) to improve the quality of the prediction.  In this case, we will use a range finder to find landmarks and use those landmarks to determine where we should be and correct the position.  Of course, the range finder is not a perfect sensor and has Gaussian noise too.  This will be included in our calculations.  There are 4 parts of the update step.  The first is to calculate the difference in the measured values (from the range finder) and the predicted values from the previous step.  The h matrix, or measurement matrix, puts the states from the last step into the same space as the measurement values.  Then, we also need to calculate the Kalman gain.  This gain is a matrix that tells us how much we want to use the new measurement to update the prediction.  It is calculated using the sensor covariance matrix, the estimate covariance matrix and the Jacobian of the h matrix, H.  Using the residual and the Kalman Gain, we update the state prediction.  Finally, we updated the covariance matrix, using the Kalman Gain and H matrix.  The actual formulas are laid out below.

Y = Z - h(X(k))
K = P^(k+1)*H*(H*P^(k+1)*transpose(H) + R)^-1
X(k+1) = X^(k+1) + K*Y
P(k+1) = (I - K*H)*P^(k+1)

In order to make the landmark detection work, the x and y positions of the landmarks were augmented to the states matrix. X.  By adding those values, the Kalman Filter became an EKF and many other matrices had to be changed, as well.   The reason for doing this, is to keep track of the landmarks and allow them to make changes to the prediction, only if they are seen.  In my case, they are always seen, but in an real-world scenario, the range finder might not be able to see all of the landmarks or misses them.

Here are some results of my work.  A typical run can be seen below.  In this image, the actual position of the robot is in blue, the initial prediction is in green and the final prediction (after landmark detection with 20 landmarks) is in red.  The robot tracks the random path very well over 2 minutes, with a time step of 0.1 seconds.

The error between the actual and updated paths for this run can be seen below.  There was an average RMS error of 3.45 units over the course of the path.  What is neat, is that the Kalman Filter seems to correct itself when there is a lot of error. If odometry was the only sensor used, the error would grow much faster, and it would not correct itself.